10655. Вирусное дерево 2

Вам дано дерево с n вершинами и n – 1 ребрами. Вершины пронумерованы от 1 до n, i-ое ребро соединяет вершины a_i и b_i.

У Вас имеется k цветов. Для каждой вершины в дереве Вы выбираете один из k цветов для ее покраски, чтобы выполнялось следующее условие:

· Если расстояние между двумя разными вершинами x и y меньше или равно двум, то x и y имеют разные цвета.

Сколько существует способов раскрасить дерево? Найдите ответ по модулю 10⁹ + 7.

Вход. Первая строка содержит два числа n и k (1 ≤ n, k ≤ 10⁵). Каждая из следующих n – 1 строк содержит два целых числа a_i и b_i (1 ≤ a_i, b_i ≤ n).

Выход. Выведите количество способов раскрасить дерево по модулю 10⁹ + 7.

Пример входа 1	Пример выхода 1
4 3 1 2 2 3 3 4	6
Пример входа 2	Пример выхода 2
5 4 1 2 1 3 1 4 4 5	48

РЕШЕНИЕ

графы – поиск в глубину

Анализ алгоритма

Начнем раскраску дерева с вершины 1. Ее можно покрасить k цветами.

Пусть мы находимся в вершине v. Если она не имеет предка (v = 1), то сыновей можно раскрасить k – 1 цветами. Если вершина v имеет предка, то ее сыновей можно покрасить k – 2 цветами. Поскольку расстояние между сыновьями вершины v равно 2, то их нельзя раскрашивать одинаковыми цветами.

Пусть для определенности вершина v имеет предка. Тогда первого сына v можно покрасить k – 2 цветами, второго сына k – 3 цветами и так далее.

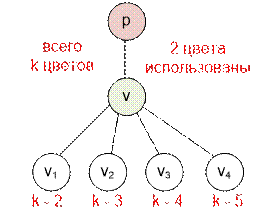
Остается перемножить количества цветов, которыми можно раскрасить каждую вершину.

Пример

Для первого примера имеется 6 способов раскраски:

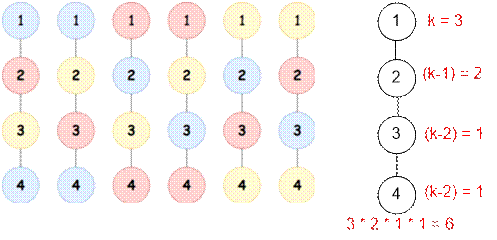
Рассмотрим второй тест. Возле каждой вершины укажем количество цветов, которыми ее можно раскрасить. Например, вершину 5 можно раскрасить 2 цветами, так как ее цвет не должен совпадать с цветами вершин 1 и 4. Общее количество способов раскрасить дерево равно 4 * 3 * 2 * 1 * 2 = 48.

Реализация алгоритма

Входной граф храним в списке смежности g. Объявим константу – модуль MOD.

#define MOD 1000000007

vector<vector<int>> g;

Функция dfs возвращает количество способов раскрасить дерево с корнем в вершине v по модулю MOD = 10⁹ + 7. Предком вершины v является p. Вершину v можно покрасить col цветами.

int dfs(int v, int col, int p = -1)

{

long long res = col;

Мы находимся в вершине v. В переменной cnt отмечаем количество цветов, которыми нельзя красить сыновей вершины v. Изначально установим cnt = 1, так как сыновья вершины v не могут иметь цвет вершины v. Если вершина v имеет предка (p ≠ -1), то сыновья вершины v также не могут иметь цвет предка v.

int cnt = 1;

if (p >= 0) cnt++;

Перебираем сыновей to вершины v.

for (int to : g[v])

if (to != p)

{

Вершина to может быть покрашена k – cnt цветами. С каждым сыном значение cnt будет увеличиваться на 1.

res = (res * dfs(to, k - cnt, v)) % MOD;

cnt++;

}

return res;

}

Основная часть программы. Читаем входные данные.

scanf("%d %d", &n, &k);

g.resize(n + 1);

for (i = 0; i < n - 1; i++)

{

scanf("%d %d", &a, &b);

g[a].push_back(b);

g[b].push_back(a);

}

Запускаем поиск в глубину из вершины 1. Вершину номер 1 можно покрасить k цветами.

res = dfs(1, k);

Выводим ответ.

printf("%lld\n", res);

Python реализация

Установим максимальную глубину стека интерпретатора Python.

import sys

sys.setrecursionlimit(1000000)

Объявим константу – модуль MOD.

MOD = 1000000007

Функция dfs возвращает количество способов раскрасить дерево с корнем в вершине v по модулю MOD = 10⁹ + 7. Предком вершины v является p. Вершину v можно покрасить col цветами.

def dfs(v, col, p = -1):

res = col

Мы находимся в вершине v. В переменной cnt отмечаем количество цветов, которыми нельзя красить сыновей вершины v. Изначально установим cnt = 1, так как сыновья вершины v не могут иметь цвет вершины v. Если вершина v имеет предка (p ≠ -1), то сыновья вершины v также не могут иметь цвет предка v.

cnt = 1

if p >= 0: cnt += 1

Перебираем сыновей to вершины v.

for to in g[v]:

if to != p:

Вершина to может быть покрашена k – cnt цветами. С каждым сыном значение cnt будет увеличиваться на 1.

res = (res * dfs(to, k - cnt, v)) % MOD

cnt += 1

return res

Основная часть программы. Читаем входные данные.

n, k = map(int, input().split())

g = [[] for _ in range(n + 1)]

for _ in range(n - 1):

a, b = map(int, input().split())

g[a].append(b)

g[b].append(a)

Запускаем поиск в глубину из вершины 1. Вершину номер 1 можно покрасить k цветами.

res = dfs(1, k)

Выводим ответ.

print(res)